TensorFlow编程策略
TensorFlow名称由来
TensorFlow中的计算过程都可以表示为一个计算图(computation graph),又称有向图(directed graph),其作用与外观都可以比作程序流程图。在计算图中我们能直观地观察数据的计算流程,换个说法,你可以观察到“张量在这其中流动的过程”。
计算图中的每一个运算操作被叫做一个节点(Node),每一个节点可以有任意的输入和任意的输出。如果一个运算的输入取值自另外一个运算的输出,那么称这两个运算存在依赖关系。存在依赖关系的两个节点通过边(Edge)互相连接。
张量(Tensor)就是在边中流动(Flow)的数据。其数据类型可以是任意的。这也是TensorFlow名称的由来。
计算图:TensorFlow的计算模型
接触计算图
在TensorFlow中,计算图是神经网络计算的流程的直观表示。计算图被定义为有向图,其中节点对应于数学运算。 在数学上,计算图是表达和评估数学表达式的一种方式。
接下来通过简单的举例对计算图进行描述:
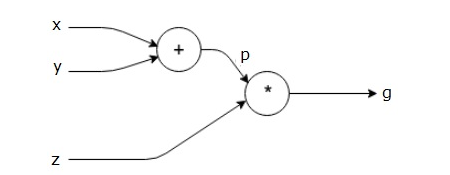
首先我们尝试表示
上面的计算图具有一个加法节点(具有“+”符号的节点),其具有两个输入变量x和y以及一个输出q。
第二个例子:
多层全连接网络的计算图
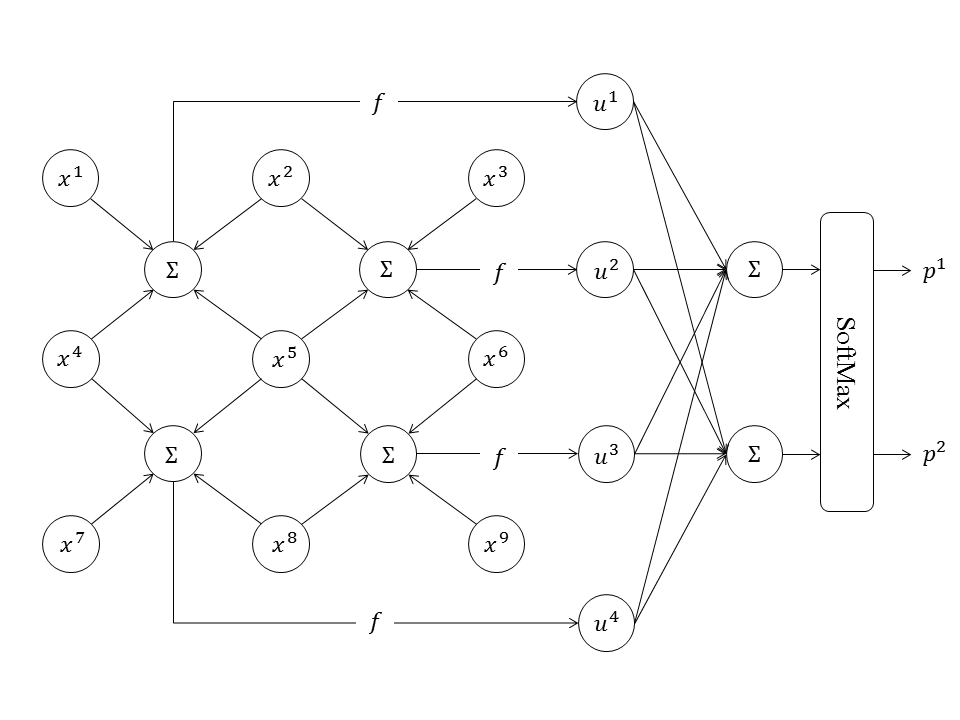
常见的多层全连接神经网络示意图就是一个计算图,它的节点都是标量,表示计算的粒度较细。现在我们可以用向量节点更简洁地表示多层全连接神经网络,如下图所示。
计算图可以灵活地表示更为复杂的神经网络:
计算图和向前传播
实际上,计算图本身就表示着正向传播。比如在上面的图中我们表示了。如果我们对这些变量进行取值:x = 1和y = 3的值来获得p = 4,然后p = 4和z = -3来得到g = -12。
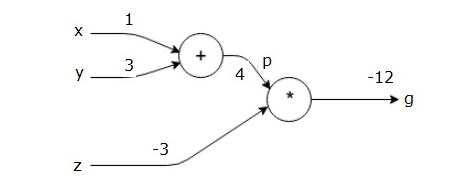
上图是这个过程表示在计算图中。所以,计算图本身就很直观的表示了向前传播。
计算图中的反向传播
反向传播的目的是计算每个输入相对于最终输出的梯度。例如,在简单的表达式中,我们看到两组x和y之后,就可以解出k和b来。之后我们可以用这组k和b来预测不知道的x对应的y。这便是机器学习任务最直观的解释。所以这些梯度对于使用梯度下降训练神经网络至关重要。
诶嘿嘿其实我才写了一点...